Faraday's Law of Induction
This is part of the HSC Physics course under the topic Electromagnetic Induction.
HSC Physics Syllabus
- analyse qualitatively and quantitatively, with reference to energy transfers and transformations, examples of Faraday's Law and Lenz's Law `\varepsilon = -N (∆\phi)/(∆t)`, including but not limited to:
Faraday's Law of Induction
This video will analyse qualitatively and quantitatively examples of Faraday's Law. It introduces the equation `\varepsilon = -N (∆\phi)/(∆t)`.
Discovery of Electromagnetic Induction
Michael Faraday wrapped wires around opposite ends of a soft iron ring, with one attached to a power source and another to a voltmeter. After the switch is closed, the current through the first wire caused a temporary pulse of induced current to be created in the opposite wire, which was detected by the voltmeter.
This is because the first wire's current created a magnetic field, which caused the free moving electrons (unaffected by potential difference) in the opposite wires to experience a magnetic force.
$$F=qvB\sin{\theta}$$
This movement of electrons is an electric current. However, after a short while, the movement of electrons will stop as the constant force causes them to end up in a particular extremity of the conductor e.g. one end of a straight conductive rod. Thus, a current is only induced when the magnetic field, experienced by the conductor is changing.
This is called Faraday’s Law of Induction, which states that an electromotive force (EMF) is induced in a conductor when it experiences change in magnetic flux. In any closed electrical conductor, this EMF leads to a current. The magnitude of the EMF is proportional to the rate of magnetic flux change. Faster the change, greater the induced current.
Induced EMF due to Faraday's Law is given by:
$$\varepsilon = -N\frac{\Delta \phi}{\Delta t}$$
where:
- ɛ is the induced EMF, also the potential difference or voltage created due to electromagnetic induction (unit: V)
- `N` is the number of turns of coil that experience the changes in flux
- `\Delta \phi` is the change in magnetic flux in Wb
- `\Delta t` is the period of time (in seconds) over which the change in flux occurs
Note the negative sign in Faraday's Law is explained in Lenz's Law.
Changes in Magnetic Flux
To understand and apply Faraday's Law, it is important to know how to calculate magnetic flux, and also identify when a change in flux has occurred.
Magnetic flux experienced by a conductor is given by:
$$\phi=B_{||}A=BA\cos{\theta}$$
where:
- `B` is the magnetic field strength in Teslas (T) or Wb m–2.
- `A` is the area of the conductor through which magnetic field lines project in metres squared (m2)
- `\theta` is the angle between the magnetic field lines and the normal area of the area

Any changes to the area, magnetic field strength and angle `\theta` results in a change in magnetic flux passing through the given area of a conductor.
Calculation Example
A coil of 10 turns is placed in a uniform magnetic field. Initially, there is a total of 0.50 Wb of magnetic flux passing through the coil. The magnitude of the magnetic field is reduced zero at a constant rate over 1.5 seconds.
Calculate the magnitude of EMF induced in the coil.
Solution:
The 10 turns of coil experiences a decrease in magnetic flux because the magnetic field strength decreases.
$$\varepsilon = -N\frac{\Delta \phi}{\Delta t}$$
$$\varepsilon = -(10)\frac{0 - 0.50}{1.5}$$
$$\varepsilon = 10 \text{ V}$$
Practical Investigation For Faraday's Law
Demonstrating Faraday's Law can be effectively done using a simple setup involving a permanent magnet and a coil of wire. Here’s how it works and the factors that affect the magnitude of the induced EMF.
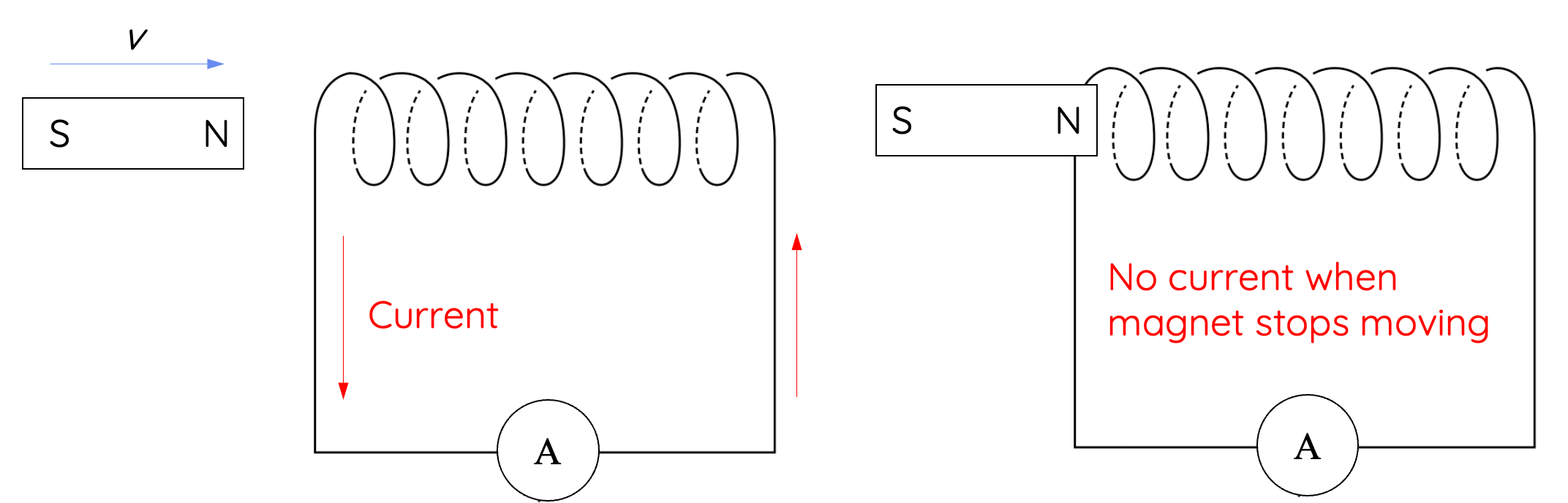
- Movement of Magnet: The demonstration involves moving the magnet in and out of a copper coil with multiple turns or moving the coil around the magnet. This movement changes the magnetic field through the coil.
- Induction of EMF: As per Faraday’s Law, this change in magnetic field induces an EMF in the coil. The EMF can be measured by connecting the coil to a sensitive voltmeter. The current due to this induced EMF can be measured using a sensitive ammeter or galvanometer.
The factors that affect the magnitude of induced EMF can be found in the equation:
$$\varepsilon = -N\frac{\Delta \phi}{\Delta t}$$
- Magnetic Field Strength (`B`): A stronger magnetic field from the permanent magnet means a greater magnetic flux, which can induce a higher EMF when changed.
- Speed of Movement: The faster the magnet is moved in and out of the coil (or the coil around the magnet), the greater the rate of change of the magnetic flux (`\frac{\Delta \phi}{\Delta t}`), thereby inducing a higher EMF.
- Number of Turns in the Coil (`N`): More turns in the coil increase the coil’s ability to intercept the magnetic field lines, thus inducing a greater EMF for the same rate of change in magnetic flux.
- Orientation of the Coil: The angle at which the coil is positioned in relation to the magnetic field affects the amount of flux going through it. The most effective induction occurs when the plane of the coil is perpendicular to the magnetic field lines.
- Cross-Sectional Area of the Coil: Larger coils with bigger cross-sectional areas can intercept more magnetic flux, thus inducing a greater EMF.
Previous section: Faraday's Law of Induction
Next section: Lenz's Law