Full-flight Projectile Motion: Maximum Height, Time of Flight and Range

 

This topic is part of the HSC Physics syllabus under the section Projectile Motion.

HSC Physics Syllabus

  • Apply the modelling of projectile motion to quantitatively derive the relationships between the following variables:

– maximum height
– time of flight
– final velocity
– horizontal range of the projectile

    • Solve problems, create models and make quantitative predictions by applying the equations of motion relationships for uniformly accelerated and constant rectilinear motion

    Projectile Motion: Time of Flight, Maximum Flight and Range

    Maximum Height

    The maximum height of an object’s projectile motion is the point at which it reaches the highest vertical displacement during the projectile motion. In other words, it is the maximum point of the parabolic path.

    Maximum height of a projectile is affected by initial launch height and initial vertical velocity. It is not affected by initial horizontal velocity.

     

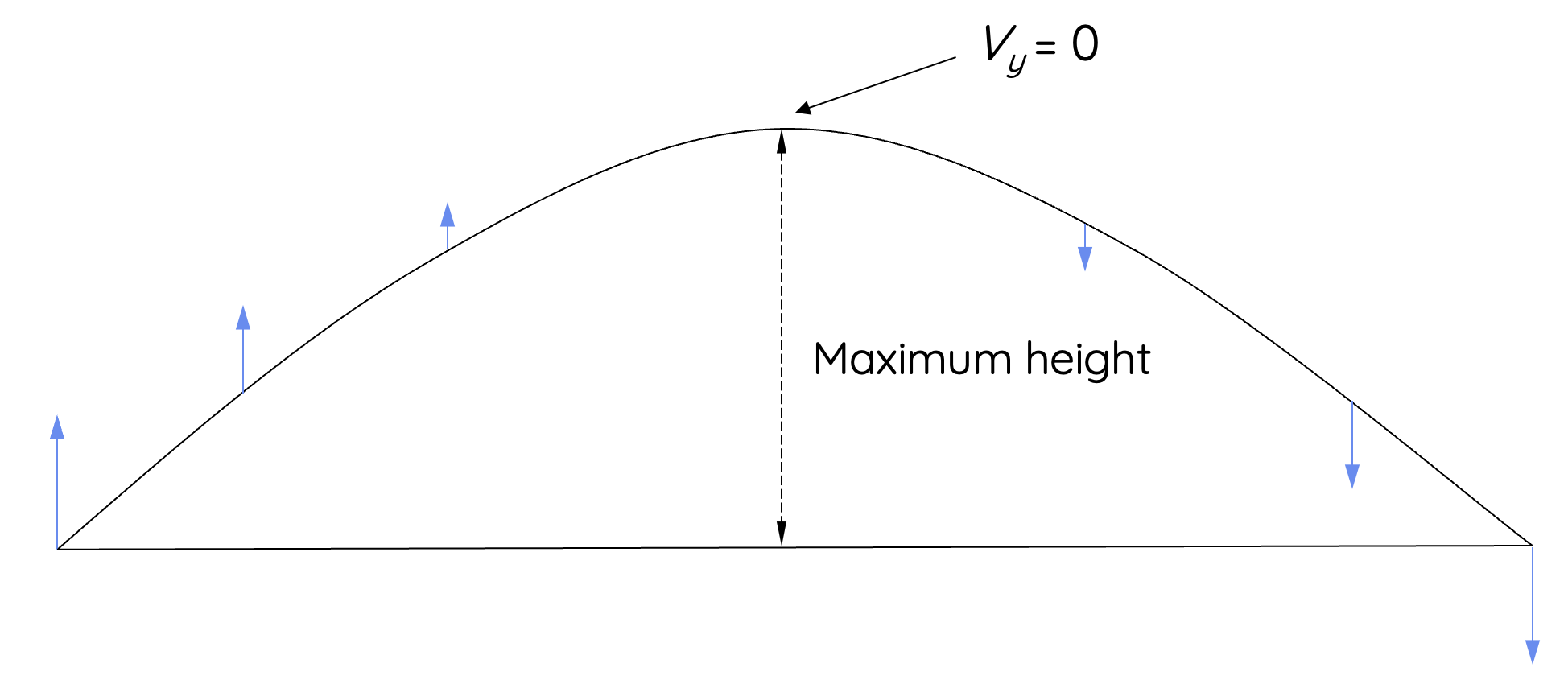
    Maximum height of projectile motion

     

    At maximum height, the vertical component of velocity equals zero. Thus, the instantaneous velocity at the maximum height equals to the horizontal component of velocity.

      Calculating maximum height is usually associated with the following rectilinear equation:

       

        `v_y^2=u_y^2+2a_ys`

        Time of Flight

        Time of flight refers to the duration of the entire projectile motion: from the time of launch to the time when it reaches its destination. Time of flight is affected by initial vertical component velocity. It is not affected by initial horizontal component of velocity.

        Calculating time of flight is usually associated with the following equation:

         `s=u_yt+1/2a_yt^2`

         

        Range

        At completion of motion, the horizontal displacement of the projectile is referred to as the range. The range or horizontal displacement is affected by the object’s initial horizontal velocity and time of flight. Since time of flight of projectile motion is affected by the vertical component of initial velocity, range is indirectly affected by initial vertical velocity.

        Since horizontal velocity is never concerned with acceleration, range or horizontal displacement is calculated using the simple relationship between distance, speed or time:

        $$s_x = u_xt + \frac{1}{2}a_xt^2$$
        `a_x` = 0:
          
        $$\Delta x = u_x t_\text{flight}$$

        Example 1

        A projectile is launched at 100 m s-1 at an elevation of 45º relative to the ground.

        (a) Calculate the vertical component of its velocity.

        (b) Calculate the time of flight of the projectile.

        (c) Calculate the maximum height of the projectile above its launch position. 

        (d) Calculate the range of the projectile.

         

        Solution to part (a):

         `u_y=usintheta`
         
        `u_y=100sin45^o`
         
        `u_y=70.7  ms^-1`

         

        Solution to part (b):

        `s=u_yt+1/2a_yt^2`

        At the completion of projectile motion, the vertical displacement s is 0:

         `0=(70.7)t+1/2(-9.8)t^2`
         
        `0=70.7t-4.9t^2`
         
        `0=t(70.7-4.9t)`
         
        `t=0` or `t=14.4` seconds
         
        Time of flight = 14.4 seconds. t = 0 corresponds to when the object is about to be launched.
         

        Solution to part (c): 

        `v_y^2=u_y^2+2a_ys`

         

        At maximum height, vertical velocity = 0:

        `(0)^2=(70.7)^2+2(-9.8)s`
         
        `s=(70.7)^2/(2xx9.8)` 
         
         `s=255`
         

        Maximum height = 255 m above ground

         

        Solution to part (d):

        `Deltax=u_x*t_(flight)`

        In order to calculate the range, initial horizontal velocity is required.

        `u_x=ucostheta`
         
        `u_x=100cos45^o`
         
        `u_x=70.7  ms^-1`
        Calculate range:
         
        `Deltax=(70.7)*(14.4)`
         
        `Deltax=1020` m

          

        This is what the projectile motion looks like:

         

        Example 2

        A cricket ball was thrown with an initial velocity, `U` = 15.0 m s-1 at an angle of elevation of 35º, as shown in the diagram below.

          

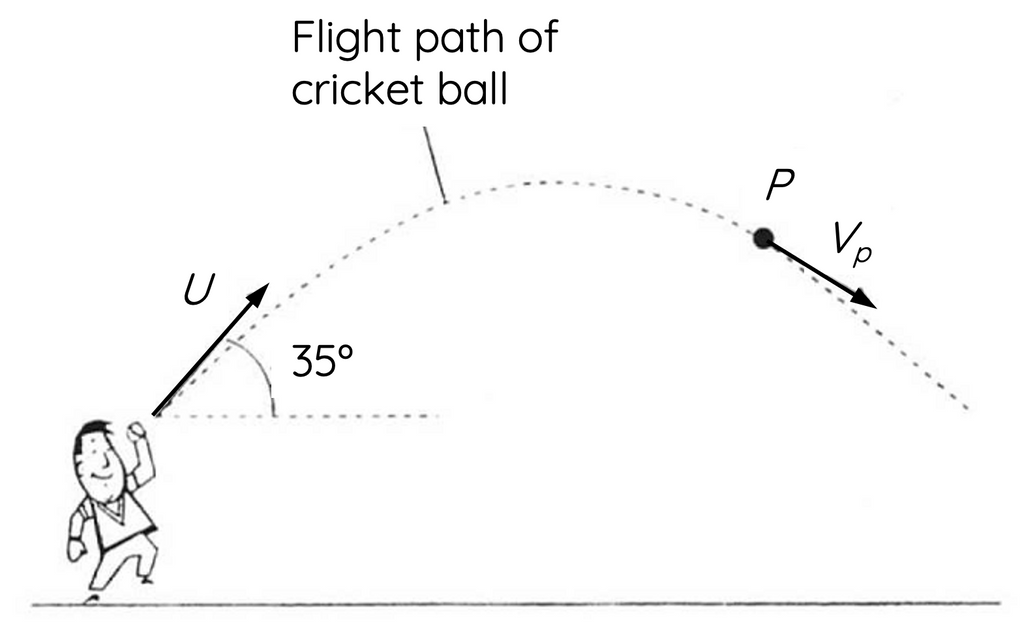
        Projectile motion question

          

        At point `P` in the flight, a remote sensor measured the vertical component of the velocity of the ball to be 6.7 m s-1 downwards. 

        Calculate the magnitude and direction of the instantaneous velocity. `V_p`, of the cricket ball when it is at point, `P`, in the flight.

         

        Solution:

        Since we are given the vertical velocity at point `P`, we will need to find the horizontal component to find `V_p`.

        The horizontal component remains constant throughout projectile motion. The initial horizontal velocity is:

        `u_x=15cos35º`

         

        `u_x=12.3` m/s

         

         

        Using Pythagoras's theorem to calculate velocity at point P:

         

        `V=sqrt(12.3^2+(-6.7)^2)`
         
        `V=14.0` m/s
         
        To find the direction, we will need to use trigonometry:
         
        `tantheta=6.7/12.3`
         
        `theta=tan^-1(6.7/12.3)`
         
        `theta=28.6º`
         
        Therefore, the the cricket ball is travelling at 14.0 m/s at an angle of 28.6º below the horizontal.