Newton's Law of Gravitation
This topic is part of the HSC Physics syllabus under the section Motion in Gravitational Fields.
HSC Physics Syllabus
-
Apply qualitatively and quantitatively Newton’s Law of Universal Gravitation to:
Gravitational Force and Acceleration
Newton’s Law of Universal Gravitation
Newton's Law of Universal Gravitation states that every mass attracts every other mass in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
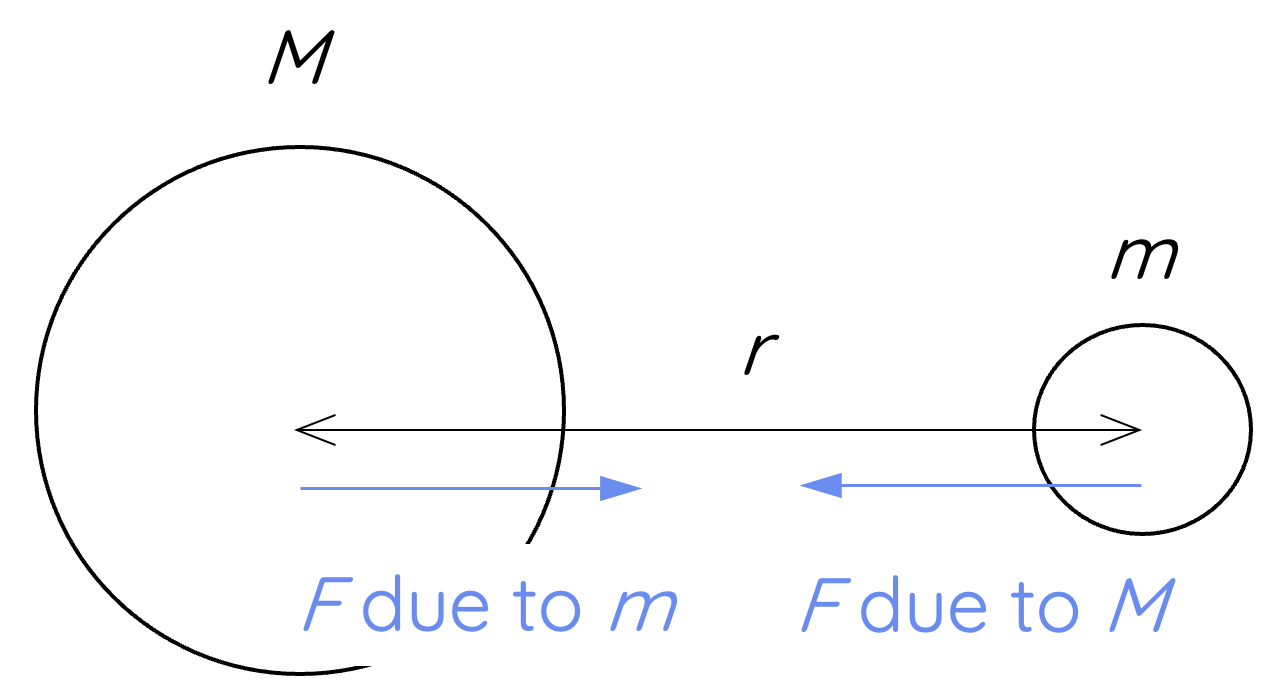
Quantitatively, this is expressed in the formula:
`F_g=(GMm)/r^2`
where:
- `F` is the gravitational force (in N) between two masses `M` and `m` (in kg)
- `G` is the universal gravitational constant = `6.67 xx 10^{-11}`
- `r` is the distance between the centres of the masses in metres (m).
The most important application of this law is the concept of gravity or weight force. Gravity arises from the gravitational attraction between Earth and a mass in its gravitational field. Thus, when calculating the force of gravity, `M` and `m` are the mass of Earth and the mass experiencing the force of gravity respectively.
Example 1
Discuss the following situations with regards to gravitational force.
(a) If the distance between two masses is doubled, find the change of the force.
(b) If the mass of one object is doubled, find the change of the force.
Example 2
Calculate the gravitational force that exists between a 70 kg person and a 1000 kg car that is parked 2.0 m away.
Example 3
Calculate the force of gravity that is exerted on Earth by the Sun.
Use the following information in your calculations:
- Mass of Sun = `2.0 ×x 10^30` kg
- Mass of Earth = `6.0 ×x 10^24` kg
- Distance between Sun and Earth = `1.5 × 10^8` km
Gravitational Field Strength
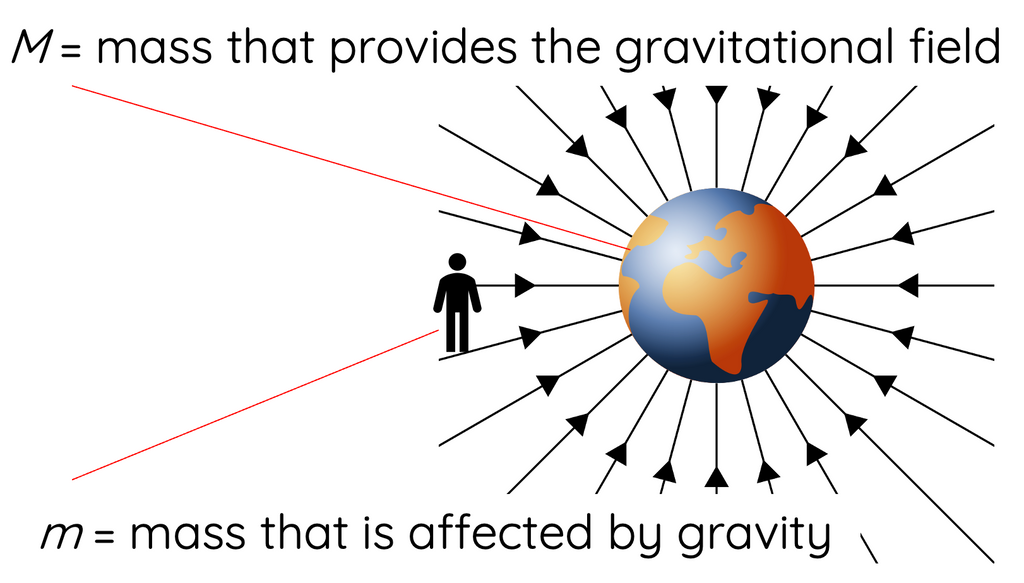
By applying Newton’s second law `F = ma`, we can determine the acceleration an object is experiencing due to the force of gravity.
where:
- `g` is the gravitational acceleration (also known as gravitational field strength)
- `G` is the universal gravitational constant = `6.67 xx 10^{-11}`
- `M` is the mass of the object that exerts the force of gravity
- `r` is the distance between the centres of the masses in metres (m).
Gravitational Field of Earth
We can use the formula to calculate the average value of `g` on the surface of Earth.
Using the following values from the NESA HSC Physics data sheet:
- Mass of Earth = `6.0 xx 10^24 \text{kg}`
- Average radius of Earth: `6.371 xx 10^6 \text{m}`
Factors That Affect Gravitational Field Strength
$$g = \frac{GM}{r^2}$$
Gravitational field strength is directly proportional to the mass of the object that provides the field e.g. Earth, and inversely proportional to the square of the distance from the mass.
There are several factors which influence the value of `g`:
Altitude
As altitude increases, the distance from the Earth's centre also increases. Since gravitational force is inversely proportional to the square of the distance between two masses, the value of g decreases with altitude. This means the gravitational field strength is lower on top of mountains.
Latitude
The Earth is not a perfect sphere; it's an oblate spheroid, meaning it's slightly flattened at the poles and bulging at the equator. Therefore, the radius of the Earth is larger at the equator than at the poles.
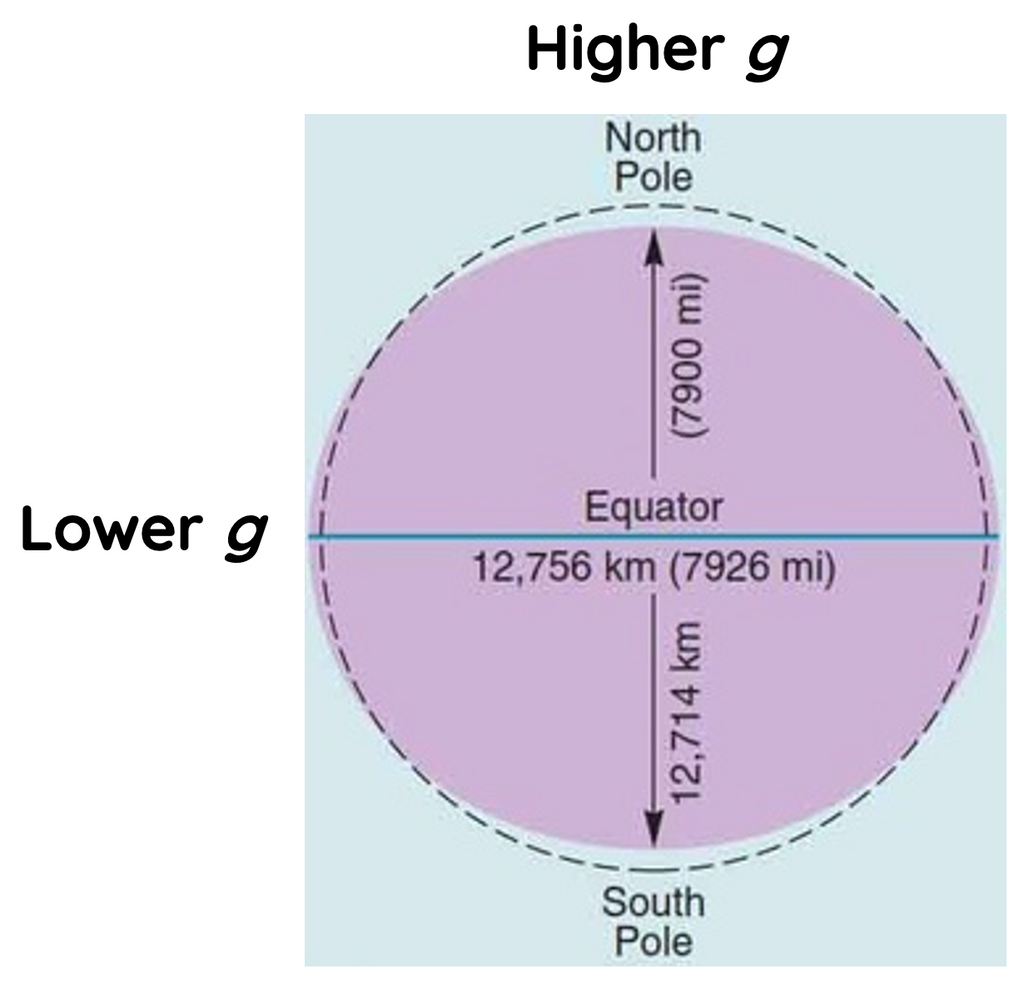
Due to the Earth's rotation, there's a centrifugal force that acts outwardly at the equator but is absent at the poles. This force reduces the effective gravitational pull experienced at the equator.
As a result, g is slightly larger at the poles (where the radius is smaller and there's no centrifugal reduction) and smaller at the equator.
Crust Density
The density of the Earth's crust is not uniform. Different regions have varying densities due to different geological formations like mountains, plateaus, ocean trenches, etc.
Areas with higher density exert a greater gravitational pull, leading to slight increases in g values, known as positive gravitational anomalies. Conversely, regions with lower density, such as oceanic trenches, exhibit lower g values, or negative gravitational anomalies.
Example 3
Explain how the acceleration due to gravity varies according to the planet’s altitudes.
Next section: Orbital Motion and Velocity of Satellites