Radioactive Decay
This topic is part of the HSC Physics course under the section Properties of the Nucleus.
HSC Physics Syllabus
- analyse the spontaneous decay of unstable nuclei, and the properties of the alpha, beta and gamma radiation emitted (ACSPH028, ACSPH030)
Radioactive Decay
This video discusses different types of radioactive decay and their properties, including
- Alpha decay
- Beta minus decay
- Beta plus decay
What is Radioisotope?
Recall:
- A nuclide is an atom or nucleus characterised by a specific number of protons and neutrons.
- Isotopes are nuclides with the same number of protons but different number of neutrons. For example, U-238 and U-234 are isotopes of uranium because they both contain 92 protons but different number of neutrons.
A radioactive isotope or radioisotope is an isotope of an element that is unstable and hence will undergo radioactive decay to achieve greater nuclear stability.
What is Radioactive Decay?
Radioactive decay is a nuclear transmutation process through which an unstable nucleus achieves greater stability.
Nuclear transmutation is a process through which the number of protons and neutrons in a nucleus changes.
The nuclide before a transmutation is called the parent nucleus. The new nuclide formed after a transmutation is called the daughter nucleus.
There are four types of radioactive decay:
- Alpha decay
- Beta minus decay
- Beta plus decay
- Gamma decay
Alpha Decay
Alpha decay involves the emission of an alpha particle (helium nucleus). Since a He-4 nucleus consists of two protons and two neutrons, the atomic number of the daughter nucleus decreases by 2, and its atomic mass decreases by 4.
The total binding energy of products is greater than the binding energy of the parent nuclide, which causes alpha decay to be exothermic.


Alpha decay typically occurs for radioisotopes that have too many nucleons, such as those with atomic numbers greater than 83.
On a neutron vs proton number graph, alpha decay will shift the nuclide towards the bottom left, towards the zone of stability.
Beta Minus Decay
Beta-minus decay involves the emission of an electron and an antineutrino. During this transmutation, a neutron is converted into a proton, raising the atomic number by 1 while keeping the atomic mass number constant.
The binding energy of the daughter nuclide (product) is greater than that of the parent nuclide, which causes beta minus decay to be exothermic.


Beta minus decay typically occurs in radioisotopes whose neutron to proton ratio (n/p) is too high. By converting a neutron to a proton, the n/p ratio of the daughter nuclide decreases.
On a neutron vs proton number graph, beta minus decay moves a nuclide towards the bottom right of the graph, towards the zone of stability.
Beta Plus Decay
Beta plus decay involves the emission of a positron and a neutrino. Beta plus decay is less common than beta minus decay. During the transmutation, a proton is converted into a neutron, reducing the atomic number by 1 while keeping the atomic mass number constant.
The binding energy of the daughter nuclide (product) is less than that of the parent nuclide, which causes beta plus decay to be endothermic.


Beta plus decay typically occurs in radioisotopes whose neutron to proton ratio (n/p) is too low. By converting a proton into a neutron, the n/p ratio of the daughter nuclide increases.
On a neutron vs proton number graph, beta plus decay moves a nuclide towards the top left of the graph, towards the zone of stability.
Gamma Decay
Gamma decay involves the emission of gamma photons to allow nuclides to reach a lower energy state. Gamma decay usually co-occurs with alpha and beta decays as they produce nuclides in excited states. Nuclides with excessive energy reach a lower energy state through emission of gamma photons. Gamma decay is exothermic.
Unlike other types of radioactive decay, gamma decay does not change the nuclear composition of the nuclide.

For example, cobalt-60 undergoes beta-minus decay to form nickel-60 while emitting an electron and an antineutrino in the process.

The nickel-60 nuclide is currently in an excited state and will emit a gamma photon of 1.17 MeV of energy to reach a lower energy state.

This is followed by another gamma decay (emission of 1.33 MeV photon) to reach the ground state.

Sometimes, the first stage of gamma decay is absent as cobalt-60 can emit a beta particle of higher energy (happens 0.12% of the time).
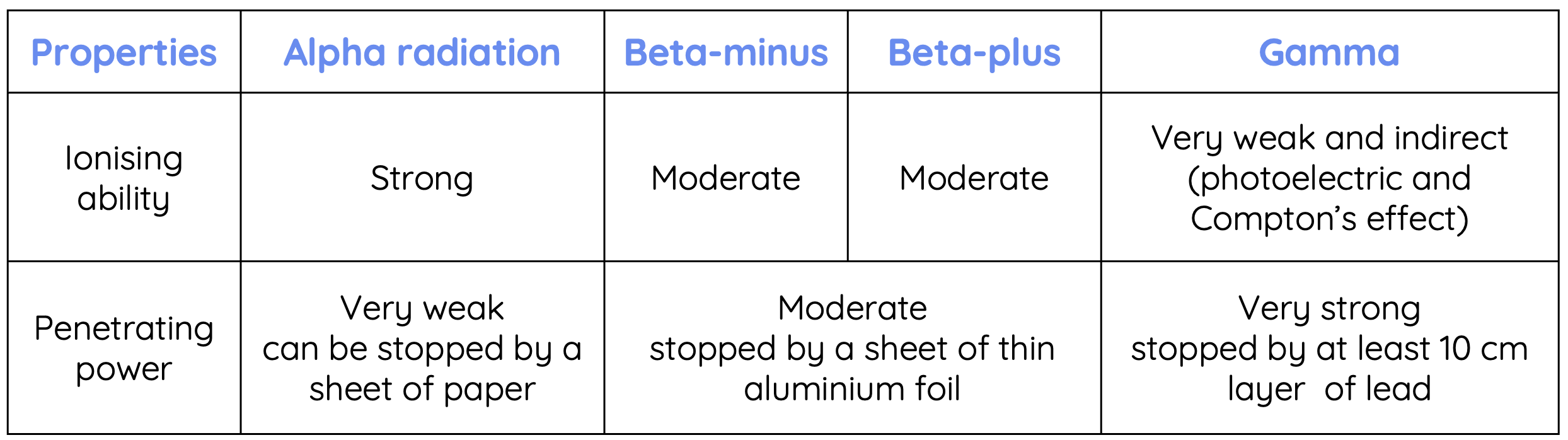
Properties of Alpha, Beta and Gamma Radiation
Alpha, beta and gamma radiation differ in their charge and mass. In electric and magnetic fields, alpha particles experience smaller deflection compared to beta particles due to their greater mass. In contrast, gamma radiation is not affected by electric and magnetic fields because they are uncharged.

Alpha, beta and gamma radiation also differ in terms of their ionising ability and penetrating power. Ionising ability refers to the ability of a radiation to cause neutral atoms to become charged ions. Penetrating power measures how easily the radiation passes through matter.
Previous section: Introduction to Nuclear Physics
Next section: Radioactive Decay Calculations
BACK TO MODULE 8: FROM THE UNIVERSE TO THE ATOM