Special Relativity – Relativistic Momentum
HSC Physics Syllabus
- describe the consequences and applications of relativistic momentum with reference to:
– `p_v=(m_0 v)/sqrt((1-v^2/c^2 ))`
– the limitation on the maximum velocity of a particle imposed by special relativity (ACSPH133)
Consequences and Applications of of Relativistic Momentum
This video discusses the concept of relativistic momentum as another implication of special relativity. The video also explains why there is a maximum limit on the speed of masses.
Mass Dilation
To a stationary observer, the mass of a particle travelling at relativistic velocity becomes heavier (dilated).
Implications of mass dilation
- The main implication of mass dilation is that more energy is required to accelerate a body when its mass becomes so large at relativistic velocities.
- The energy required to accelerate a body to the speed of light is infinitely large, thus deeming the process impossible. This implication is demonstrated in particle accelerators whereby theoretical calculations indicate that to accelerate an electron to the speed of light would require more energy than what is available in this universe.
- Einstein also stated that the speed of light is the absolute limit in the universe in which it cannot be reached and exceeded. As time becomes slower at relativistic speeds, it would theoretically come to a halt at the speed of light. When time stops, the concept of speed (distance over time) becomes incomprehensible.
Relativistic Momentum
As the velocity of a mass increases, its momentum increases according to classical Newtonian momentum equation p = mv. However, classical momentum theory becomes inconsistent with experimental data when a body is travelling at relativistic velocities.
Classical theory of momentum:
![]()
Relativistic momentum according to special relativity

- where pv is the relativistic momentum of a particle or body measured and observed from a moving frame of reference (or stationary observer’s perspective).
- m0 is the mass of the body measured by an observer in the rest frame. Rest frame is defined as a reference frame in which the observer is moving at the same velocity as the observed body.
- v is the relative velocity of the body as observed by a stationary observer.
- Relativistic momentum is measured using a body’s rest mass (m0) so the increase in momentum is only due to the increase in the body’s velocity.

- Speed of light is the absolute limit of any body’s velocity. No objects in the universe can exceed this limit. While this imposes a limit on classical momentum (p = mv), relativistic momentum, in contrast, approaches to infinity as the velocity of a body approaches the speed of light.
Relativistic Momentum vs Classical Momentum
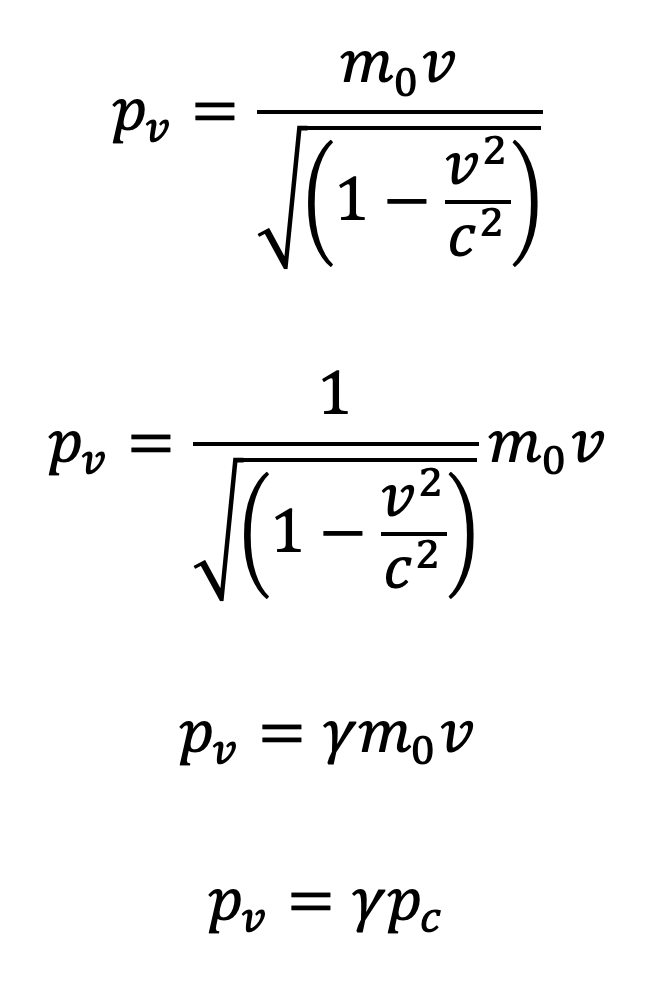
Relativistic momentum = relativistic constant ✕ classical momentum
- where γ = relativistic constant (Lorentz transformation)

When velocity of the observed body is small, relativistic momentum and classical momentum are very similar because is γ close to 1.

Even when a body is travelling at 0.10c, its relativistic momentum from Newtonian momentum would only differ by 0.5%. So, the consequence of special relativity on momentum is not obvious at velocities that we normally observe. Only at a velocity that is 87% of the speed of light, we would observe momentum of a particle twice as its initial.
When velocity approaches the speed of light, relativistic momentum deviates from classical momentum. It increases exponentially.
Kinetic Energy at Relativistic Velocities
Similar to momentum, kinetic energy becomes inconsistent with classical physics when a particle is travelling at relativistic velocities.

As v approaches c, the denominator becomes very small so a particle’s kinetic energy approaches infinity.
Maximum Speed Limitation of Particles
Special relativity mandates that objects with mass cannot reach nor exceed the speed of light.
This can be understood in three ways:
- As a mass's velocity approaches c, its mass and momentum approach infinity. According to Newton's second law (F = ma), an infinitely large force is then required to maintain a constant acceleration to enable the particle to reach c.
- As a mass's velocity approaches c, its kinetic energy approaches infinity. By the law of conservation of energy, this would require an infinite amount of work to be done on the particle.
- As a mass's velocity approaches c, its dimension in the same plane of motion measured by a stationary observer approaches zero (length contraction). The dimension would equal to zero if v = c.
In all three cases, the requirement for a particle to reach c is physically impossible and would break existing laws of physics.
Previous section: Time Dilation and Length Contraction
Next section: Energy-mass Equivalence