Schrödinger's Model of the Atom & SPDF Notation
This is part of preliminary HSC Chemistry course under the topic of Atomic Structure and Atomic Mass.
HSC Chemistry Syllabus
- Model the atom's discrete energy levels, including electronic configuration and SPDF notation (ACSCH017, ACSCH018, ACSCH020, ACSCH021)
- Investigate energy levels in atoms and ions through:
Schrödinger's Model & SPDF Notation
Schrödinger Quantum Mechanical Model
Erwin Schrödinger proposed a model to elucidate the behaviour of electrons in an atom. Instead of tracing a precise path of electrons around the nucleus (like in Bohr's model), he applied mathematical equations to predict the probability of finding an electron in a particular space – the orbital. In some diagrams, the probability of finding an electron is represented by the density of the electron cloud. The greater the density of this electron cloud reflects an increased probability of finding an electron.

What are Electron Orbitals?
Schrödinger's wave equation treats electrons not as particles orbiting the nucleus in fixed paths, but as wave-like entities with probabilistic distributions. An orbital is defined as the region in space around the nucleus where there is a high probability (typically 90-95%) of finding an electron.
Unlike the defined paths (orbits) in Bohr's model, orbitals describe areas where electrons are likely to be found. This is often represented by electron cloud diagrams, where the density of the cloud indicates the probability of finding an electron.
Schrödinger's model introduces four quantum numbers to describe the properties of these orbitals and the electrons within them:
- Principal Quantum Number (`n`): Indicates the energy level and relative size of the orbital. It can take positive integer values (1, 2, 3, ...).
- Angular Momentum Quantum Number (`l`): Defines the shape of the orbital and can take values from 0 to `n-1` for each value of `n`. Each value of `l` corresponds to a specific type of orbital (s, p, d, f).
- Magnetic Quantum Number (`m_l`): Describes the orientation of the orbital in space and can take integer values from `-l` to `+l`, including zero.
- Spin Quantum Number (`m_s`): Specifies the electron's spin direction, which can be either +1/2 or -1/2.
Note: the knowledge of quantum numbers is not explicitly outlined by the HSC Chemistry syllabus but may be taught in some cases.
SPDF Orbitals and Sub-orbitals
Electrons exist in shells (orbitals) denoted by the principal quantum number (n = 1, 2, 3...) which corresponds to the energy state described in Bohr's model of the atom. Each shell, barring the first one, contains several sub-shells (sub-orbitals) or energy sub-levels. An electron's location is described by its shell and a specific sub-shell (s, p, d, f), within which it occupies an orbital. The sub-shell is determined by an electron's angular momentum quantum number (`l`).
Each sub-shell, with the exception of `s` orbitals, is further divided into various orientations. The orientation of a sub-shell is determined by an electron's magnetic quantum number (`m_l`). Every orientation of a sub-orbital or sub-shell can contain up to two electrons.
The following diagram shows different types of orbitals, sub-orbitals and their various orientations.

- The `s` sub-shell, the lowest energy level, contains one `s`-orbital and can accomodate 2 electrons.
- The `p` sub-shell, the next energy level, contains three `s`-orbitals (`p_x`, `p_y`, and `p_z`), each oriented differently at right angles to each other. This sub-shell can accomodate 6 electrons.
- The `d` sub-shell, the third energy level, contains five `d`-orbitals, and can accommodate 10 electrons. The `d`-orbitals have complex shapes.
- The `f` sub-shell, the fourth energy level, contains seven `f`-orbitals, and can accomodate 14 electrons. The `f`-orbitals, too, have complex shapes.
The follow table outlines the relationship between the principal quantum number of a shell and the numbers of sub-shells, orbitals and electrons.
|
Principal quantum number (n) |
Number of sub-shells |
Types of sub-shells |
Number of orbitals in each sub-shell |
Maximum # electrons in each sub-shell |
Maximum # electrons in the shell |
|
1 |
1 |
S |
1 |
2 |
2 |
|
2 |
2 |
S P |
1 3 |
2 6 |
8 |
|
3 |
3 |
S P D |
1 3 5 |
2 6 10 |
18 |
|
4 |
4 |
S P D F |
1 3 5 7 |
2 6 10 14 |
32 |
SPDF Electron Configuration
The SPDF electron configuration provides a systematic method for noting the positions of all the electrons in an atom. The arrangement of electrons in an atom's orbitals is subject to three guiding principles:
Pauli Exclusion Principle
- No two electrons in the same atom can have identical values for all four of their quantum numbers. The implication of this principle is that any given orbital can accommodate a maximum of two electrons, and these electrons must have opposite spins.
- The concept of 'spin' refers to an inherent property of electrons, which can be either 'up' or 'down.
Aufbau Principle
- Electrons fill the available orbitals starting from the lowest energy level.
- All orbitals within a particular energy level possess the same energy. For instance, the three `2p` orbitals are equivalent in terms of energy.
Hund's Rule
- For orbitals of the same energy, electrons fill each orbital singly before any orbital gets a second electron.
- Electrons preferentially occupy individual orbitals rather than sharing orbitals.
Orbital Diagrams
The diagram presented is known as an orbital diagram, a tool that facilitates the modelling and visualisation of the spatial distribution of orbitals within a certain electron configuration. Starting from the bottom, the level marked '1' represents the lowest energy state.
Each horizontal line, denoted as '_', signifies an orbital. As we can observe, there's one orbital in the `s` subshells, three orbitals in the `p` subshells, and so forth. Owing to the Pauli Exclusion Principle, each orbital can accommodate a maximum of two electrons.
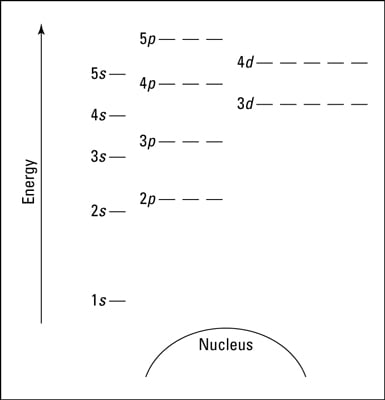
Hence, the electron capacity of each energy level increases progressively: the first level can hold 2 electrons, the second level can accommodate 8 electrons (`2s` and `2p`), the third level has room for 18 (`3s`, `3p` and `3d`), and so on. This ascending pattern continues in accordance with the increasing number of orbitals and subshells in each subsequent energy level. In addition, the maximum number of electrons in each energy level is consistent with the rule outlined in Bohr's model of the atom (2, 8, 18, 32...).
This sequence of electron filling the orbitals according to Aufbau principle can be illustrated on the periodic table.

Examples of SPDF Configuration and Orbital Diagram
Let's use some examples to deepen your understanding.

- Consider hydrogen atom, with an atomic number of 1. Its solitary electron must occupy the lowest energy orbital, which is the `1s` orbital. Therefore, its electron configuration is written as `1s^1`.
- Similarly, helium atom, which has 2 electrons, has an electron configuration of `1s^2`.
- Lithium atom, with 3 electrons, has an electron configuration of `1s^2 2s^1`. The third electron will reside in the `2s` sub-orbital which has the second lowest energy level after the `1s` sub-orbital.
- Boron atom, with 5 electrons, has an electron configuration of `1s^2 2s^2 2p^1`. The `2p` orbital has the lowest energy level after the `2s` sub-orbital.

- Carbon atom, with 6 electrons, has an electron configuration of `1s^2 2s^2 2p^2`. By Hund's rule, the second electron in the `2p` orbital will occupy a separate sub-orbital such that the two electrons are unpaired. This is better demonstrated in the orbital diagram.
- Nitrogen atom, with 7 electrons, has an electron configuration of `1s^2 2s^2 2p^3`. Since the `p` orbital has three different orientations, the third electron will occupy a separate sub-orbital such that all three electrons are unpaired.
- Oxygen atom, with 8 electrons, has an electron configuration of `1s^2 2s^2 2p^4`. Since all three `2p` orbitals already contains 1 electron, the fourth electron must be paired in one of the three orbitals.
Electron Configurations Using Noble Gases
Noble gas electron configuration is a shorthand notation used in writing the electron configuration of an element, where the electron configuration of the noble gas prior to the element. This method simplifies the notation by taking advantage of the fact that noble gases have complete electron shells, which makes them particularly stable.
For example, the electron configuration of
- sodium atom would be [Ne] `3s^1`
- calcium atom would be [Ar] `4s^2`
Electron Configurations of Ions
Atoms form cations and anions when they lose and gain electron(s) respectively. This means ions have different electron configurations to their corresponding atoms.
For example for sodium atom and cation:
- Na atom: [Ne] `3s^1`
- Na+ ion: [Ne] or `1s^2 2s^2 2p^6`
For example for oxygen atom and oxygen anion:
- O atom: `1s^2 2s^2 2p^4`
- O2– ion: `1s^2 2s^2 2p^6`
In the two examples above, the sodium and oxygen ions have different atomic numbers but the same electron configuration.