Thomson's Discovery of The Electron
This topic is part of the HSC Physics course under the section Structure of The Atom.
HSC Physics Syllabus
-
investigate, assess and model the experimental evidence supporting the existence and properties of the electron, including:
How Did Thomson Discover The Electron?
This video describes Thomson's experiment that led to the discovery of the first subatomic particle – the electron.
J.J. Thomson’s Experiment
Thomson's experiment involved manipulating the path of a cathode ray using a uniform electric field and a uniform magnetic field. Thomson's experiment obtained a value for the charge to mass ratio of cathode rays, which proved their particle nature.

In the first part of Thomson's experiment, a pair of charged metal plates was used to create a uniform electric field. When a cathode ray travelled through this field, it was deflected towards the positive plate.
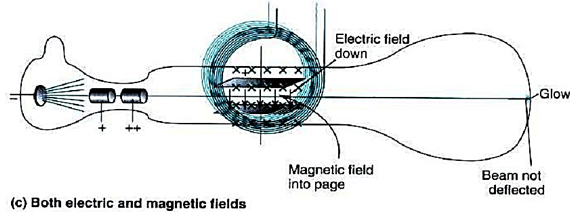
Next, Thomson applied a uniform magnetic field using current-carrying coils. The direction of this magnetic field was perpendicular to the electric field, and positioned such that it would cause the cathode ray to deflect downwards.
Thomson adjusted the strength of the magnetic field until the cathode travelled a straight path. When this occurred, the force acting on the cathode ray due to the electric field balanced the force due to the magnetic field.
$$F_E=F_B$$
$$qE=qvB\sin\theta$$
$$E=vB$$
$$v=\frac{E}{B}$$

After a straight trajectory was achieved, the electric field was switched off. Under the influence of the magnetic field only, the cathode ray was deflected downwards. Here, the radius of the cathode's curved path can be analysed by considering centripetal force.
The centripetal force was provided by the force due to the magnetic field:
$$\frac{mv^2}{r}=qvB$$
$$\frac{mv}{r}=qB$$
Expressing v in terms of E and B
$$\frac{m(\frac{E}{B})}{r}=qB$$
$$\frac{q}{m}=\frac{E}{rB^2}$$
(We recommend understanding the derivation of the above equation to be able to provide mathematical support in exam responses)
Since the value of E, B and r were known to Thomson, the value of the charge to mass ratio of the cathode ray was calculated. This value was 1.76 x 1011 C kg–1
Thomson replicated the experiment using cathodes made from different metals and under various conditions. He showed that the value of charge to mass ratio remained constant.
Thomson's Interpretation
Since an actual charge to mass ratio value was determined for cathode rays, Thomson proved that cathode rays do indeed have mass, and hence are negatively charged particles.
In addition, the constancy of the cathode ray's charge to mass ratio shows that these negatively charged particles are present in all matter. As a result, Thomson's experiment led to the discovery of the first subatomic particle – the electron.
The charge to mass ratio of electrons was shown to be 1800 times greater than that of hydrogen ions. Thomson assumed the magnitude of charge is equal for these particles, leading to the conclusion that the mass of an electron is 1800 times smaller than a hydrogen ion.
Thomson's Model of the Atom ('Plum Pudding' Model)
The discovery of the electron as a subatomic particle led to the development of Thomson's atomic model.

A simple representation of Thomson's atomic model
In Thomson's model of the atom, negatively charged electrons are dispersed in a positive mass due to electrostatic repulsion. The electrons are held together in the atom due to their attraction to the positive mass.
One major limitation of Thomson's model is the lack of explanation for the positive mass. This feature of the model was based on theory and lacked experimental evidence.
Thomson's model of the atom was shown to be incorrect in Geiger-Marsden's gold foil experiment.
Previous Section: Cathode Ray Experiments
Next Section: Rutherford's Atomic Model
BACK TO MODULE 8: FROM THE UNIVERSE TO THE ATOM