Torque & Work Done in Circular Motion

 

This topic is part of the HSC Physics syllabus under the section Circular Motion.

HSC Physics Syllabus

  • Investigate the relationship between the rotation of mechanical systems and the applied torque:
– `tau=rFsintheta`
– `tau=r_(_|_)F`

  • Investigate the relationship between the total energy and work done on an object executing uniform circular motion

Torque and Work Done in Circular Motion

Work done in Uniform Circular Motion

During uniform circular motion, the speed of an object does not change which means its kinetic energy remains constant. 

 

`KE=1/2mv^2`

 

This also means no work is done on the object as otherwise it would accelerate while gaining kinetic energy.

 

 
 

While centripetal force acts on an object throughout uniform circular motion, it is not in the direction of its displacement so we cannot apply the formula `W=Fd` in this scenario.

The relationship between force and work done can be more accurately characterised by the following equation:

 

`W=F_c*s*costheta`

where: 

  • `theta` is the angle between direction of force and direction of displacement `s` of an object in circular motion.

In uniform circular motion, the net force (centripetal force) is acting orthogonal (90 degrees) to the object's displacement. This means `costheta` is always `cos90º` which equals zero.

Therefore, work done during uniform circular motion is zero.

You can read about and revise circular motion here

Example 1 (HSC 2004)

A car with a mass of 800 kg travels at a constant speed of 7.5 m/s on a roundabout so that it follows a circular path with a radius of 16 m.

 

 

A person observing this situation makes the following statement.

‘There is no net force acting on the car because the speed is constant and the friction between the tyres and the road balances the centripetal force acting on the car.’

Assess this statement. Support your answer with an analysis of the horizontal forces acting on the car, using the numerical data provided above.

 

Solution:

The car is undergoing uniform circular motion on a horizontal bend so it has a net force acting on it towards the centre of the circle; this net force is the centripetal force. The centripetal force is provided by the friction between the tyres of the car and the road, and is given by:

$$F_c = \frac{mv^2}{r}$$

$$F_c = \frac{(800)(7.5)^2}{16} = 2812.5 \text{ N towards the centre of circle}$$

Since this centre-seeking force acts orthogonally to the velocity of the car, no work is done and the speed of the car (hence kinetic energy) remains constant.

Therefore, the statement is incorrect.

Torque

Torque is a fundamental concept in physics and engineering, often referred to as the rotational equivalent of force. It represents the tendency of a force to rotate an object around an axis, fulcrum, or pivot. Understanding torque is crucial in many areas, from simple mechanical systems to complex engineering designs.

Torque is given by:
`tau=rFsintheta`
where: 
  • `r` is the radius of circular motion or distance between the pivot and point at which the force is applied
  • `theta` is the angle between the lever vector and applied force `F` that is causing the rotation/circular motion.

 

 

When `theta` is perpendicular, `tau=rFsintheta` becomes `tau=r_(_|_)F`. The magnitude of torque is at its maximum when the force vector is perpendicular to the lever arm as this gives the maximum value for sine function.

In non-uniform circular motion, speed is not constant because it is acted on by force(s) other than centripetal force. This force also produces torque.

Torque can be applied outside of circular motion in any situation involving turning about a pivot. 

 
 
 
Torque can be thought as the rotational analog of force. If force is a 'push or pull', then torque can be though as a twist. This is commonly applied in engineering e.g. using a wrench.
 
 
 
 
The direction of torque is determined in the same way as angular velocity `omega`, by using the right-hand grip rule.  
 

Example 2

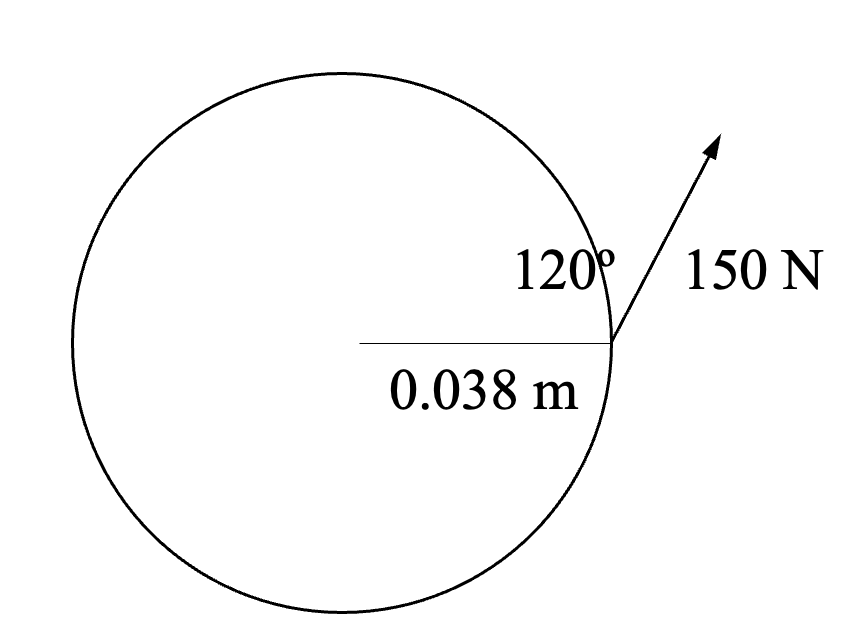
Torque Calculation Example

 

Calculate the magnitude of torque produced by opening a jar of pickles if the lid on the jar has a radius of 0.038 m and a 150 N force is applied to the lid at the angle shown. 

 

$$\tau = rF\sin{\theta}$$

$$\tau = (0.038)(150)sin{120}$$

$$\tau = 4.94 \text{ N m }$$

Example 3

A 100 g pendulum swings in a clock, never swinging past an angle of 8 degrees with the vertical. If the pendulum swings on a 2.8-meter-long string attached to a pivot, what is the maximum amount of torque about the pivot?

Example 4

Consider the following fulcrum system.

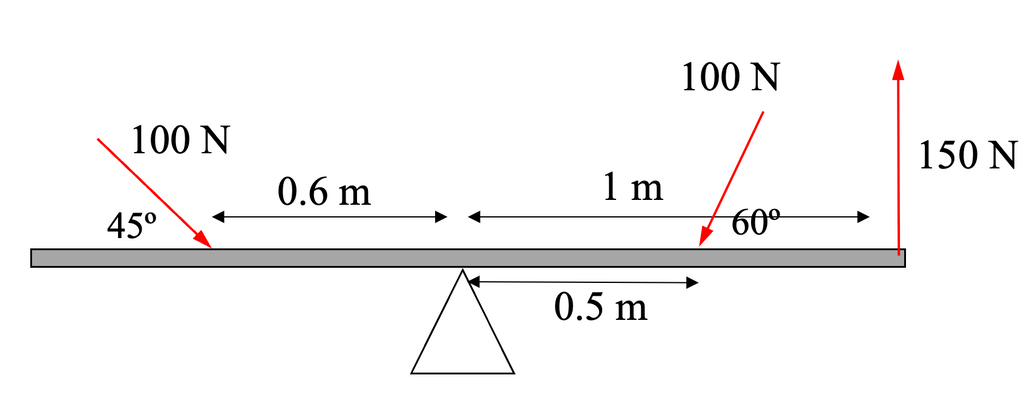
Torque and fulcrum net torque

 

Calculate the total torque and determine which direction the see-saw rotates.