Bohr's Atomic Model & Limitations
HSC Physics Syllabus
- assess the limitations of the Rutherford and Bohr atomic models
- investigate the line emission spectra to examine the Balmer series in hydrogen (ACSPH138)
- relate qualitatively and quantitatively the quantised energy levels of the hydrogen atom and the law of conservation of energy to the line emission spectrum of hydrogen using:
Bohr's Model of the Atom
What are Bohr's Postulates?

Niels Bohr proposed three postulates in his atomic model:
1. Electrons revolve around the nucleus in circular orbits with discrete radii and quantised energies. In these orbits, electrons exist in 'stationary states' and do not emit energy.
$$E_n = \frac{1}{n^2}E_1$$
Bohr’s model of the atom describes electrons orbiting in stable energy levels as opposed to Rutherford's model in which electrons' motion was not described.

2. An electron can transition between orbits by absorbing or releasing energy that is exactly equal to the difference in energy of orbits, consistent with the law of conservation of energy.
Electron excitation occurs when an electron absorbs energy to move to an orbit of higher energy.
Electron relaxation occurs when an electron moves to a lower orbit, releasing energy in the form of electromagnetic radiation (photon).
The energy of photon is given by
$$\Delta E_{orbit}=E_{final} - E_{initial}=-E_{photon}$$
If the photon's energy is less or greater than the difference in energy of orbits involved in the electron transition, no transition will occur. This interaction between electrons and energy is referred to as spectroscopy.
When electrons absorb energy to move to orbits of higher energies, absorption spectroscopy occurs. Conversely, when electrons release energy while moving to orbits of lower energies, emission spectroscopy occurs.
3. The angular momentum of an electron is quantised - it is an integral multiple of a specific value.
The angular momentum `L_n` of an electron is given by
$$L_n = \frac{nh}{2\pi}$$
where n = energy level, h = Planck's constant.
Hydrogen Spectrum and Bohr's Model of the Atom
The hydrogen emission spectrum provides evidence for Bohr's postulate and model of the atom.

Emission spectrum of heated gas. Credit: libretext
The emission spectrum of hydrogen consists of specific visible light lines on a black background. It is produced when light from a heated sample of hydrogen gas undergoes dispersion through a glass prism. This can also be produced using other gases and discharge tubes.
When electrons in hydrogen atoms absorb energy (e.g. heat), they can transition to orbits of higher energy. These excited electrons will emit energy in the form of electromagnetic radiation (photons) when moving to orbits of lower energies.
Bohr explained that the emission spectral lines are the visible light photons released when electrons return to orbits of lower energies. The emission lines have specific wavelengths as they correspond to the specific amount of energy associated with each photon emitted.
There are multiple emission lines for hydrogen (and other elements) because an Bohr-model atom consists of orbits of many energy levels, which in turn allows for electron transitions that absorb/release different amounts of energy.
 Spectral lines observed in the Balmer Series or hydrogen spectrum (part of) are a result of electronic transition from higher energy levels to n = 2.
Spectral lines observed in the Balmer Series or hydrogen spectrum (part of) are a result of electronic transition from higher energy levels to n = 2.
Electromagnetic radiation that is absorbed/released during electron transitions it not limited to visible light. For example, in a hydrogen atom, electron transitions to n = 1 orbit will produce radiation in the ultraviolet spectrum (Lyman series). Electron transitions to n = 3 orbit will produce radiation in the infrared spectrum (Paschen series).
Bohr's second postulate obeys the law of conservation of energy. The energy of photon absorbed during electron excitation equals to the energy of photon emitted when the electron returns to its original orbit.
The Balmer Series
The Balmer series refers to the emission spectral lines of hydrogen in the visible light range. The Balmer series is formed when electrons transition from an orbit of higher energy to n = 2 orbit.
The Balmer series can be easily visualised by dispersing light produced from either heated hydrogen gas or hydrogen gas in a discharge tube.

Table shows the energy difference, wavelength and colour associated with each electron transition of the Balmer Series
|
Transition of n |
3→2 |
4→2 |
5→2 |
6→2 |
7→2 |
8→2 |
9→2 |
∞→2 |
|
Wavelength (nm) |
656 |
486 |
434 |
410 |
397 |
389 |
384 |
365 |
|
Energy difference (eV) |
1.89 |
2.55 |
2.86 |
3.03 |
3.13 |
3.19 |
3.23 |
3.40 |
|
Colour |
Red |
Aqua |
Blue |
Violet |
Ultraviolet |
|||
Rydberg's Equation
Rydberg's equation is used to predict the wavelength of photon absorbed or emitted when an electron transitions between orbits of different energy states. The wavelength of the photon can then be used to calculate its frequency and energy.
Rydberg's equation can be derived from Bohr's second postulate - the energy of photon equals to the exact difference in the energy of orbits involved in the electron transition.

where λ is the wavelength of emitted radiation, R is Rydberg’s constant (1.097x107 m-1), nf and ni are the final and initial energy level during an electron’s transition respectively.
The accuracy of prediction made by Rydberg’s equation decreases as the atom becomes larger. Hence, it should only be used for the hydrogen atom.
Rydberg's Equation Example
Hydrogen shows a large number of spectral lines, the visible ones being part of the Balmer series where nf = 2.
Calculate the frequency of photons emitted when electrons move from ni = 3 to nf = 2 orbit.
Using Rydberg's equation:

Since
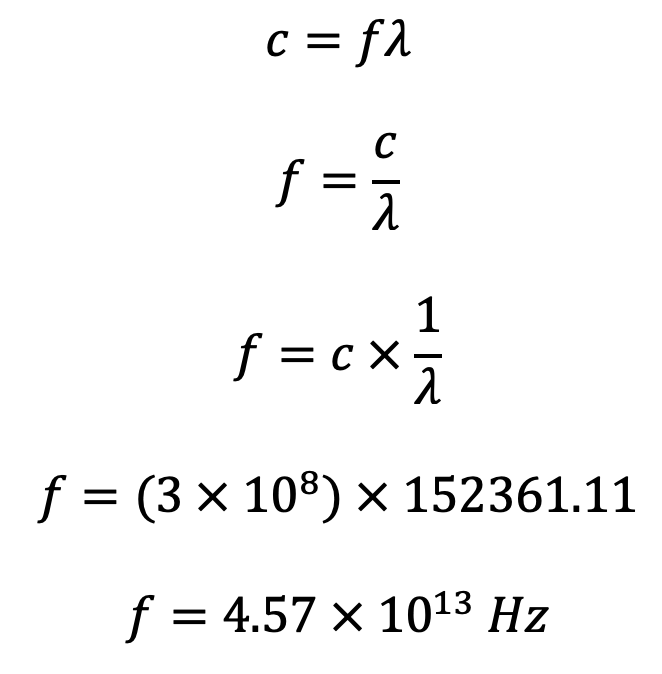
What is the energy associated with this photon?
$$E=hf$$
$$E=(6.626 \times 10^{-34})(4.57 \times 10^{13})$$
$$E=3.03 \times 10^{-20} J$$
Limitations of Bohr's Atomic Model
Bohr's model of the atom has several limitations.
- Bohr's model combines principles from both classical and quantum physics. Circular motion of electrons is from classical physics while the quantisation of its momentum and energy of orbits is from quantum physics.
- Bohr does not provide an explanation to 'stationary states' of electrons. In other words, his model does not explain why electrons can remain in their orbits without spiralling into the nucleus due to electrostatic attraction.

- Bohr's model cannot predict the relative intensity (brightness) of the spectral lines.
- Predictions made by Bohr’s model is only accurate for the hydrogen atom. The accuracy decreases as the effective nuclear charge of an atom or ion increases (due to greater number of protons).
- Each spectral line, when examined at higher magnification, actually consists of a number of smaller fine lines. These are referred to as hyperfine spectral lines. Bohr's model does not explain the presence of hyperfine lines.
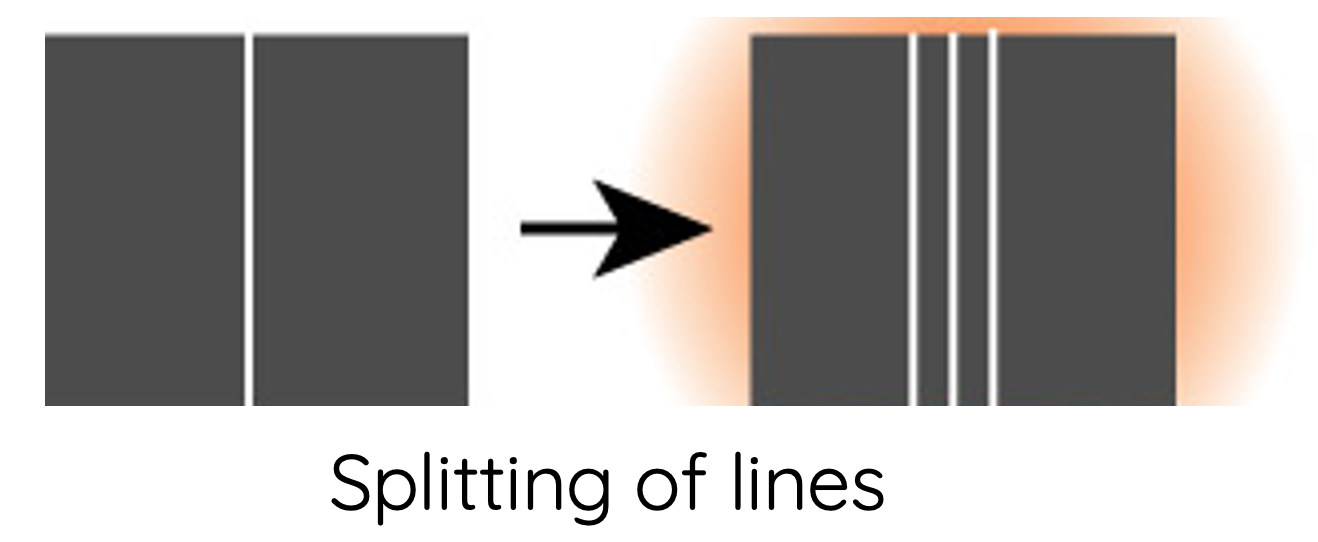
- Spectral lines undergo splitting when a sample of gas is affected by an electric field (Stark effect) and magnetic field (Zeeman effect). Bohr's model and postulates do not explain this phenomenon.
Previous section: Rutherford's Atomic Model and The Geiger-Marsden Experiment
Next section: de Broglie's Matter-waves
BACK TO MODULE 8: FROM THE UNIVERSE TO THE ATOM