HSC Physics – HOW TO: Evaluate the impact of Planck’s quantum theory
Planck’s quantum theory is undeniably the foundation of quantum physics – an important area of modern physics.
This guide aims to consolidate your knowledge from HSC Physics Module 7 (The Nature of Light) and 8 (From the Universe to the Atom) while assisting you to write cohesive and insightful responses for extended response questions related to Planck’s quantum theory.
HSC Physics – Quantum Theory
Planck hypothesised that black body radiation consists of small packets of energy known as a quantum. Each quantum's energy is dependent on its frequency (and wavelength):
`E=hf`
Planck devised the quantum theory to resolve experimental problems that could not be explained by the classical theory of physics – which predicted that intensity of black body radiation would increase to infinity with greater frequency.
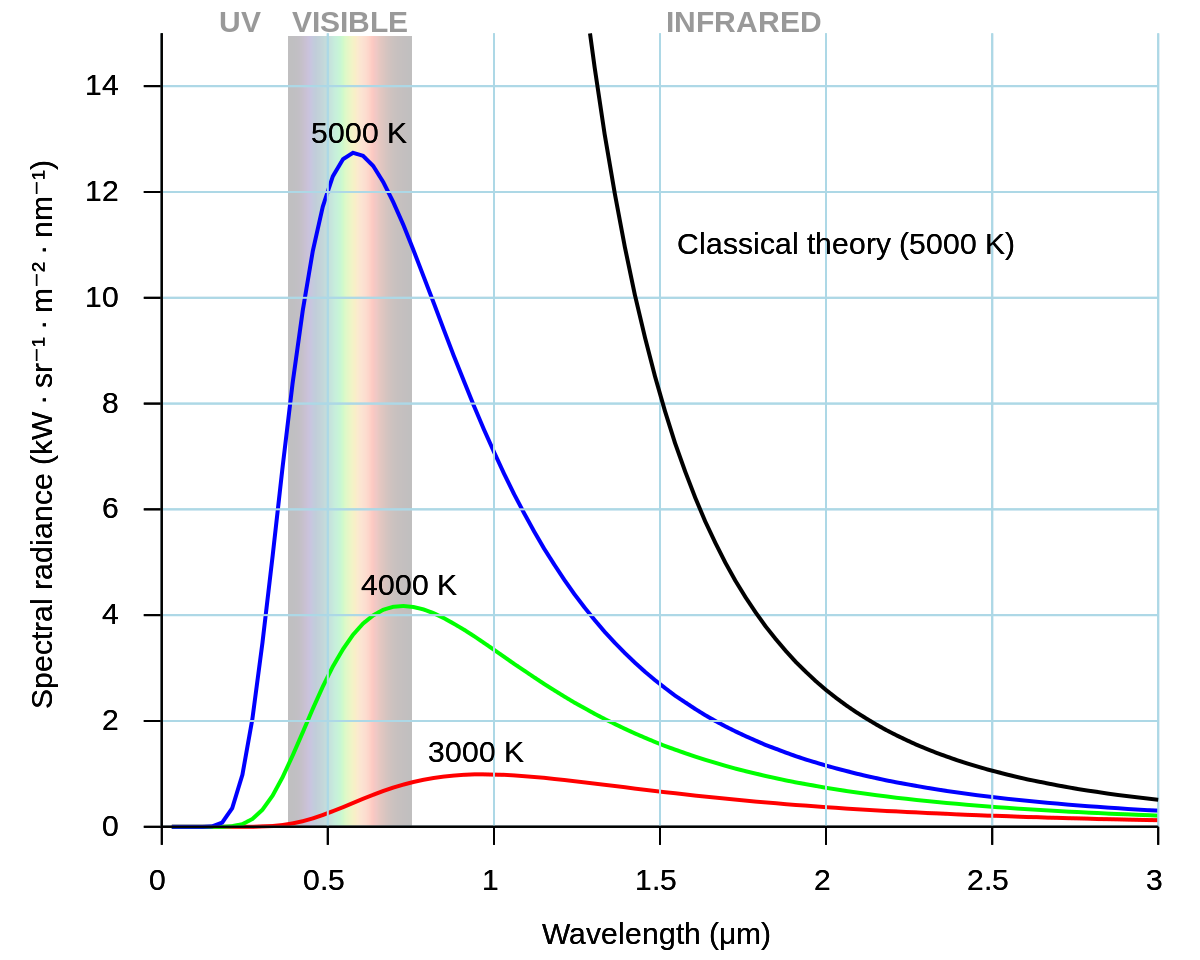
This conundrum was referred to as the ultraviolet catastrophe because the experimental result diverged from classical physics’ prediction in the ultraviolet region of the electromagnetic spectrum.
HSC Physics – Wien’s Displacement Law
Around the same time, Wien conducted experiments with black body radiation and produced results that supported Planck’s hypothesis. He demonstrated that black body radiation is in fact, like Planck suggested, discrete and finite.
Wien showed that for every radiation emitted by a black body, there is always a specific wavelength with the highest intensity. This is the dominant wavelength.
He furthered deduced that the dominant wavelength of radiation emitted by a black body is inversely proportional to temperature. Higher the temperature, shorter the dominant wavelength. This is Wien’s Displacement Law.
While Wien’s Displacement Law is not a new inclusion in the 2019 HSC Physics curriculum, its relationship with and impact on Planck’s quantum theory are definitely emphasised in the current syllabus.
HSC Physics – Quantum Model of Light
In both the old and new HSC Physics syllabi, the photoelectric effect has been and is taught closely alongside Planck’s quantum theory.
A few years after Planck’s hypothesis, Einstein used the quantum theory to develop the quantum model of light.

The quantum model of light was used to explain the Photoelectric effect. Einstein explained that energy transfer between a photon (packet of light energy) and an atomic electron is always one-to-one.
This particular explanation is not only significant in the validation of quantum theory but also our understanding of light’s nature.
This marked the turning point of classical theory of physics which comprises from the work of James Maxwell (electromagnetism) and Isaac Newton (mechanics).
HSC Physics – Models of the Atom
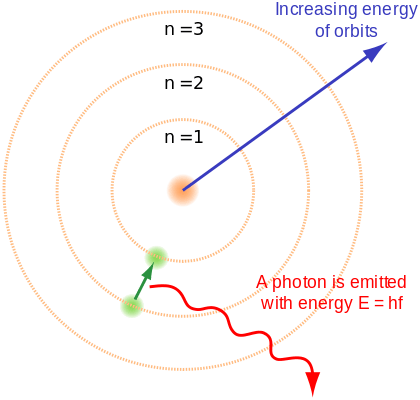
Planck’s quantum theory is also present in the Bohr model of the atom. Bohr’s third postulate claims that the angular momentum of an electron in its stable energy orbit is quantised.
In other words, the magnitude of an electron’s angular momentum must always be an integral number of a fixed value.
This concept was later supported by de Broglie’s matter-wave hypothesis.
`lambda=h/(mv)`
Since `nlambda=2pir`:
Quantitatively, de Broglie's matter-wave duality equation shows that the angular momentum of an electron (`mvr`) equals an integral n multiple of a specific value (`h/(2pi)`).
The quantisation of angular momentum showed that quantisation is ubiquitous, extending far beyond just black body radiation and light (electromagnetic waves).
As outlined by the HSC Physics syllabus, the development of the Schrödinger model of the atom could not have been possible without de Broglie’s work.
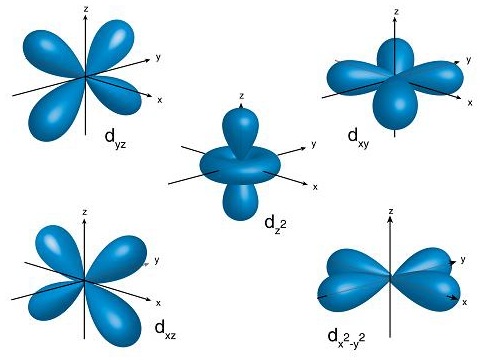
Diagram shows the 5 d orbitals whose weird shapes arise from electrons' angular momentum.
Electrons’ quantised angular momenta were used to predict the shape and size of p, d and f orbitals, all of which constitute our modern understanding of electrons.
HSC Physics – Spectroscopy
After Einstein’s explanation of the Photoelectric effect and Bohr’s atomic model, physicists, particularly astrophysicists, started to understand spectroscopy more clearly.

Quantum theory allowed us to understand the differences between emission & absorption spectra and a continuous spectrum of black body radiation.
Scientists realised that specific spectral lines absent or present in absorption and emission spectra are caused by the interaction between photons and electrons. This interaction, as proposed by Einstein earlier, is also quantised.
As a result of this new understanding, stars’ absorption spectra were recognised as a valuable source of information on stars’ surface temperature, distance from Earth, velocity and chemical composition.
Therefore, the impact of Planck’s quantum theory is also present in the field of astrophysics.
HSC Physics – Fundamental Particles
Robert Millikan in the early 20th century, in his famous oil-drop experiment, also showed that electric charge is quantised by nature.
Standard Model of Matter 
Further investigation of matter using particle beams such as the electron revealed that protons and neutrons are in fact not fundamental particles.
Baryons are quantised in the sense that they consist of an integral number of quarks.
Hadrons are made of exactly 3 quarks while mesons are made of exactly 2 quarks.
So, why is the fundamental basis of nature associated with these two integers?
Well, this is where the frontier of quantum/particle physics is at the moment
Summary
After reading this, hopefully you’ve realised the broad impact of Planck’s quantum theory.
Although Planck’s work is only covered in Module 7: The Nature of Light, its impact is also evident in Module 8: From the Universe to the Atom.
Quantum theory has been critical in our understanding of electromagnetic waves, stars, atoms and sub-atomic particles.